The Secrets of SHM: The Importance of Understanding and Physics Formulae.
What is simple harmonic motion?
What are the formulae for SHM?
Three main things describe how something moves when it does SHM: displacement, velocity, and acceleration. Displacement is how far the thing is from its normal position (either in the y or x direction), velocity is how fast the displacement changes and acceleration is how fast the velocity changes. These things change with time and can be written using math functions, such as sine and cosine.
How are the formulae for SHM made?
To make the formulae for SHM, we need to use some basic mathematics. Mathematics is the study of the relationships between numbers and patterns. We can use mathematics to model the motion of something that does SHM as analogous to circular motion.
So now we need to find the x and y coordinates of the dot. To find these values, we need to go back to the basics of mathematics and see how these functions are derived from the properties of circles and triangles. In chapter 6 of her book Is Maths Real? Eugenia Cheng explains how to understand formulae better by using the idea of abstraction. Abstraction is the process of simplifying something by focusing on the essential features and ignoring the irrelevant details. For example, when we draw a circle, we don’t care about the thickness of the line, the colour of the paper, or the size of the circle. We only care about the shape of the circle, and the fact that all the points on the circle are the same distance from the center. This distance is called the radius of the circle, and it is an essential feature of the circle.
Similarly, when we draw a triangle, we don’t care about the angles, the sides, or the area of the triangle. We only care about the shape of the triangle, and the fact that it has three straight sides and three corners. These sides and corners are called the vertices of the triangle, and they are essential features of the triangle.
Now, we can define the functions sine, and cosine using the lengths of the sides of the triangle. Sine is the ratio of the side opposite the angle we are using, and cosine is the ratio of the side adjacent to the angle we are using. In other words, we can write:
sin(θ)=y/A
x=Acos(θ)y=Asin(θ)
 Hence, for our pendulum example, the vertical coordinate y undergoes SHM in the y direction, and the horizontal coordinate x also observes SHM, but at right angles to the y direction. We can then use calculus to find the velocity and acceleration of an object undergoing SHM, through differentiation of the displacement to find the velocity, and acceleration functions. The analogous equations for motion in the horizontal axis can be derived from the displacement equation in the x direction.
Hence, for our pendulum example, the vertical coordinate y undergoes SHM in the y direction, and the horizontal coordinate x also observes SHM, but at right angles to the y direction. We can then use calculus to find the velocity and acceleration of an object undergoing SHM, through differentiation of the displacement to find the velocity, and acceleration functions. The analogous equations for motion in the horizontal axis can be derived from the displacement equation in the x direction.As mentioned at the beginning of this blog post, in SHM, the displacement of the object from its equilibrium position in the y direction is given by:
Notice that the acceleration function is proportional to the displacement function but with a negative sign. This means that the acceleration is always opposite to the displacement, which is consistent with the restoring force that causes SHM.
What if the motion starts at the maximum displacement?
We can also simplify these formulae by using the identity
In this case, we have α=θ and β=π/2. Therefore, we can substitute these values into the formula and simplify:
π/2 − sinθsinπ/2
How does understanding the formulae for SHM help us learn better?
By deriving the formulae for SHM from mathematics, we can see how they are related to each other and to the motion of something that does SHM. We can also see how the things that affect SHM, such as amplitude, frequency, and phase, change the way something that does SHM moves. For example, we can see that:
- The amplitude is the maximum displacement of something that does SHM from its normal position, and it determines the size of the motion.
- The angular frequency is the speed of change of the angular displacement, and it determines the speed of the motion. The frequency and the period of the motion are related to the angular frequency by the formulae: and T=1/f
- The phase angle, ϕ is the starting angular displacement of something that does SHM when t=0, and it determines the position of something that does SHM at any time. The phase difference between two things that do SHM is the difference between their phase angles, and it determines how they move together or apart.
- Sine and cosine are opposite functions, which means that they are shifted by radians or from each other.
This means that the displacement and the velocity of something that does SHM are out of sync by radians or , and the displacement and the acceleration are in sync by π radians or 180∘ so have opposite signs.
- The relationship between sine and cosine indicates that when displacement is at its highest point, velocity is at its lowest point. Conversely, when displacement is at its lowest point, velocity is at its highest point. In addition, when velocity is at its lowest point, acceleration is at its highest point, and when displacement is at its highest point, acceleration is also at its highpoint but negative. Finally, when displacement is at its lowest point, acceleration is at its highest point, but it is a positive maximum.
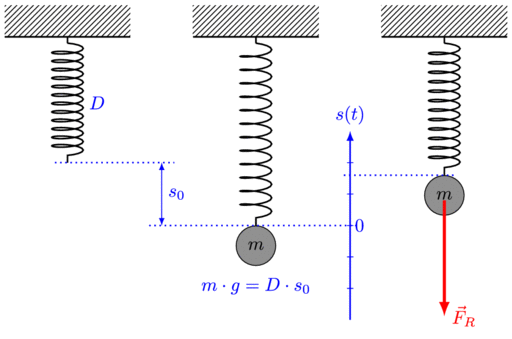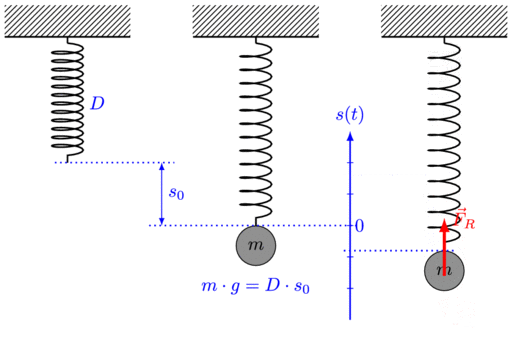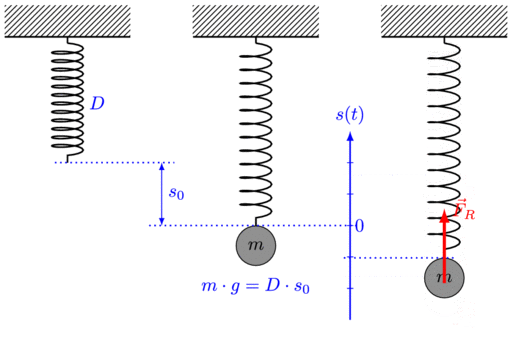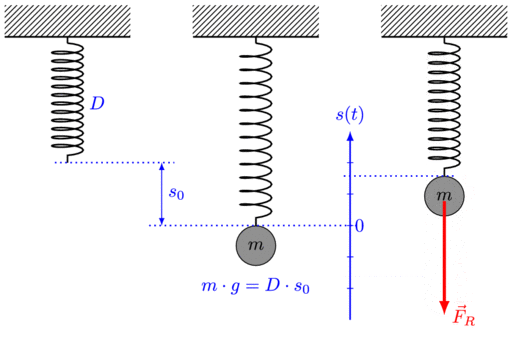







Comments